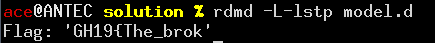Topics
Procedural content generation
|
1. Write Up: Gre-Hack CTF 2019 - Reverse - Angry Tux
This is a reverse challenge from the Gre-Hack CTF 2019.
The challenge was designed by Aleknight.
1.1. TL;DR
Some non-reversible function is applied to a 13-byte flag,
giving an 8-byte hash, which must correspond to a predefined value.
ELF headers are corrupt (no section headers) and the resulting hashed value
depends on these headers staying corrupt.
We’re given a tiny binary executable file (<700 bytes). Its ELF sections have be removed, preventing us from sending it to, say, angr.
We can open it with radare2, but the code does some unusual stuff,
like jumping out of one function. This breaks automated function analysis,
I couldn’t get r2deco to work on these ones. When run, it asks for the flag on stdin, and prints a pass/fail message.
There’s absolutely no doubt about the control flow here,
so let’s reverse the actual computation.
1.3. The actual computation
After some input/output data comparison (thanks to gdb),
I was able to rewrite a C model of what actually happens in this challenge. The flag given on stdin is passed through an Encrypt function.
First, there’s some offseting/xoring (with fixed keys, some of them directly from the ELF header, represented by image here). Then there are 5 calls to EncryptReducePass, which basically does flag[0 .. N-1] += flag[1 .. N],
and then removes the last byte. So we end up with a string shorter by 5 chars.
This might be an issue for reversing the computation.
#include <stdint.h>
/// 0x400264
uint8_t EncryptedFlag[] = { 0x43, 0x26, 0xc7, 0x31, 0x59, 0xe8, 0x9d, 0x09, };
// 0x400000
const uint8_t image[] =
{
0x7f, 0x45, 0x4c, 0x46, 0x02, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00,
0x02, 0x00, 0x3e, 0x00, 0x01, 0x00, 0x00, 0x00, 0x80, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00,
};
void EncryptXorPass(uint8_t* flag)
{
for(int i = 0; flag[i]; ++i)
flag[i] ^= 0x38;
for(int i = 0; flag[i]; ++i)
flag[i] -= image[0x18 + i % 3];
for(int i = 0; flag[i]; ++i)
flag[i] ^= image[0];
for(int i = 0; flag[i]; ++i)
flag[i] += image[1 + i % 3];
}
void EncryptReducePass(uint8_t* flag)
{
int i=0;
while(flag[i+1])
{
flag[i] += flag[i + 1];
++i;
}
flag[i] = 0;
}
void Encrypt(uint8_t* flag)
{
EncryptXorPass(flag);
for(int k = 0; k < 5; ++k)
EncryptReducePass(flag);
}
1.4. Don’t reverse, solve!
The maths here seems simple enough to be a good fit for solving.
As I mentioned, we can’t directly solve the given executable (e.g Angr),
as its headers are corrupt. Moreover, we have a C model now, we can modify it slightly so it works with
symbolic expressions instead of bytes,
and deduce the expression of the encrypted result as a function of the input.
And then, force the encrypted result to EncryptedFlag, and solve for the input. So we need an SMT solver. Here, I’m going to use STP (Simple Theorem Prover).
Our computation code, instead of actually executing arithmetic operations,
is now going to build expression trees corresponding to these arithmetic operations. Typos are easy to make, and for such computations, an error can easily make me lose one hour or more.
So I want the computation code to look, as much as possible, like the above C version. Let’s switch to D: operator overloading and garbage collection will allow us to write
expressions almost identical to the ones from the above reference model (provided a tiny STP wrapping layer).
///////////////////////////////////////////////////////////////////////////////
// Solution for the 'angry_tux' challenge from Gre-Hack 2019 CTF.
import std.format;
import std.stdio;
int main()
{
// Create a symbolic input
Expr[] flag;
foreach(i; 0 .. 13)
flag ~= symbol(format("v%02d", i));
// copy it into a work buffer
Expr[] buf = flag.dup;
// do the actual encryption
Encrypt(buf);
// require that the output of the encryption matches the expected result (aka 'EncryptedFlag')
Expr[] constraints;
for(int i=0;i < 8;++i)
constraints ~= equals(buf[i], integer(EncryptedFlag[i]));
// require the flag to start with "GH19{"
constraints ~= equals(flag[0], integer('G'));
constraints ~= equals(flag[1], integer('H'));
constraints ~= equals(flag[2], integer('1'));
constraints ~= equals(flag[3], integer('9'));
constraints ~= equals(flag[4], integer('{'));
const val = solve(flag, constraints);
writef("Flag: '");
foreach(c; val)
writef("%s", cast(char)c);
writef("'");
writeln();
return 0;
}
///////////////////////////////////////////////////////////////////////////////
// Encryption model (mimics the challenge's, but with symbolic computation)
// 0x400000:
const ubyte[] image =
[
0x7f, 0x45, 0x4c, 0x46, 0x02, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00,
0x02, 0x00, 0x3e, 0x00, 0x01, 0x00, 0x00, 0x00, 0x80, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00,
];
const EncryptedFlag = [ 0x43, 0x26, 0xc7, 0x31, 0x59, 0xe8, 0x9d, 0x09 ];
void Encrypt(ref Expr[] flag)
{
EncryptXorPass(flag);
for(int k = 0; k < 5; ++k)
EncryptReducePass(flag);
}
void EncryptXorPass(Expr[] flag)
{
foreach(ref b; flag)
b = b ^ integer(0x38);
foreach(i, ref b; flag)
b = b - integer(image[0x18 + i % 3]);
foreach(ref b; flag)
b = b ^ integer(image[0]);
foreach(i, ref b; flag)
b = b + integer(image[1 + i % 3]);
}
void EncryptReducePass(ref Expr[] flag)
{
for(int i=0; i+1 < flag.length; ++i)
flag[i] = flag[i] + flag[i + 1];
flag.length--;
}
///////////////////////////////////////////////////////////////////////////////
// Simple wrapper over STP solver, to keep the model's code readable.
import stp;
alias StpExpr = stp.Expr;
enum BITS = 8;
static VC g_vc;
static this() { g_vc = vc_createValidityChecker(); }
static ~this() { vc_Destroy(g_vc); }
class Expr
{
this(StpExpr expr) { m_expr = expr; }
Expr opShr(Expr a) { return new Expr(vc_bvRightShiftExprExpr(g_vc, BITS, m_expr, a.m_expr)); }
Expr opAdd(Expr a) { return new Expr(vc_bvPlusExpr(g_vc, BITS, m_expr, a.m_expr)); }
Expr opSub(Expr a) { return new Expr(vc_bvMinusExpr(g_vc, BITS, m_expr, a.m_expr)); }
Expr opMul(Expr a) { return new Expr(vc_bvMultExpr(g_vc, BITS, m_expr, a.m_expr)); }
Expr opAnd(Expr a) { return new Expr(vc_bvAndExpr(g_vc, m_expr, a.m_expr)); }
Expr opOr(Expr a) { return new Expr(vc_bvOrExpr(g_vc, m_expr, a.m_expr)); }
Expr opXor(Expr a) { return new Expr(vc_bvXorExpr(g_vc, m_expr, a.m_expr)); }
StpExpr m_expr;
}
Expr integer(int value) { return new Expr(vc_bvConstExprFromInt(g_vc, BITS, value)); }
Expr equals(Expr a, Expr b) { return new Expr(vc_eqExpr(g_vc, a.m_expr, b.m_expr)); }
Expr greater(Expr a, Expr b) { return new Expr(vc_bvGtExpr(g_vc, a.m_expr, b.m_expr)); }
Expr symbol(string name) { return new Expr(vc_varExpr(g_vc, (name ~ "\0").ptr, vc_bvType(g_vc, BITS))); }
int[] solve(in Expr[] vars, in Expr[] constraints)
{
vc_push(g_vc);
scope(exit) vc_pop(g_vc);
auto x = vc_varExpr(g_vc, "x".ptr, vc_bvType(g_vc, BITS));
auto equality = vc_eqExpr(g_vc, x, cast(StpExpr)vars[0].m_expr);
foreach(c; constraints)
equality = vc_andExpr(g_vc, equality, cast(StpExpr)c.m_expr);
auto not = vc_notExpr(g_vc, equality);
const ret = vc_query(g_vc, not);
assert(ret == 0);
int[] r;
foreach(v; vars)
r ~= getBVInt(vc_getCounterExample(g_vc, cast(StpExpr)v.m_expr));
return r;
}
1.5. A quick word about SMT solvers
The solve function above clearly does some non-trivial stuff. SMT solvers are actually proof-builders : you don’t tell STP "please solve this for me".
Instead, you tell it "show me that this expression is always true, regardless of the values of the unknowns".
This is what the call to vc_query does.
And the answer is either "yes it’s always true", or "no, it’s not always true, here’s a counter-example". Which means, if you want to solve for X in "X == 27 || X == 34", and that you feed this to a solver,
it’s going to answer with "no, this isn’t always true, for example, X=0 ". We’re not interested by X=0, which could also have been X=1337 or X==666, or anything other than 27 and 34. So in practice, we put a not around the whole expression, so we actually query "not(X == 27 || X == 34)".
Thus, X=0, X=1337 and X=666 aren’t counter-examples anymore. Instead, X=27 and X=34 become counter-examples, and the solutions of our initial problem.
1.6. Getting the flag
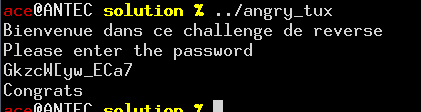
There’s a catch, though. Our encryption function is mapping 13-byte inputs to 8-byte outputs.
This means different inputs might give the same output. Indeed, the following flag is accepted, although it’s definitely not the expected one: So we need extra constraints on the input to get the intended flag.
And we know from the CTF rules that the flag must begin with "GH19{".
// require the flag to start with "GH19{"
constraints ~= equals(flag[0], integer('G'));
constraints ~= equals(flag[1], integer('H'));
constraints ~= equals(flag[2], integer('1'));
constraints ~= equals(flag[3], integer('9'));
constraints ~= equals(flag[4], integer('{'));
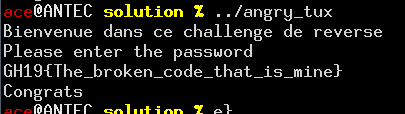
Once we add these constraints, we’re able to get a unique result from our solver! But… wait! It seems truncated! And the CTF rules are very clear:
the flag must follow the "GH19{….}" format. So, let’s complete it in the most meaningful way: Now, let’s go reap the CTF points! |