The Complexity Elephant

Thoughts about software engineering, and game development.

Topics

1. Generating mazes part 1 : using fibers to prototype the graph generation

I’m fascinated by procedural generation algorithms, especially random maze generation. This morning, I was working on a graph-based dungeon generator.

Most maze generation algorithms I know of mix the "maze logic" (i.e the graph corresponding to the maze, including doors and keys) with the "maze layout" (the spatial layout of the rooms and corridors). Actually, most of them are "maze layout" based.

Here, the idea is to start with the "maze logic", without worrying too much about the "maze layout". Spatial placement of rooms and corridors, according to a given "maze logic", will be the subject of another blog post. However, to keep things simple, I only work here with planar graphs.

Here’s how it works:

* create a planar graph
* compute a random spanning tree for this graph
* let's say you want to subdivide your maze into 4 zones (= 3 doors).
  The number of nodes per zone (NPZ) is: number of total nodes / 4.
* Repeat 3 times:
  - for each tree node N,
      compute the total count of its direct or indirect reachable children ;
      in other words, the size, in nodes, of the subtree whose root is node N, excluding nodes behind doors.
  - find the tree node N whose subtree size is the nearest of NPZ. Put a door here.
* Add some random edges (from the original planar graph), to create some cycles;
  but beware not connecting different zones.

Fine-tuning a maze generator requires the ability to see what happens between the steps. This means I’m going to need to stop the generation in the middle of the process, and display the state of the generation at the end of each step.

Here’s what the result looks like:

First, create a random planar graph. I do this by Delaunay-triangulating a bunch of random positions.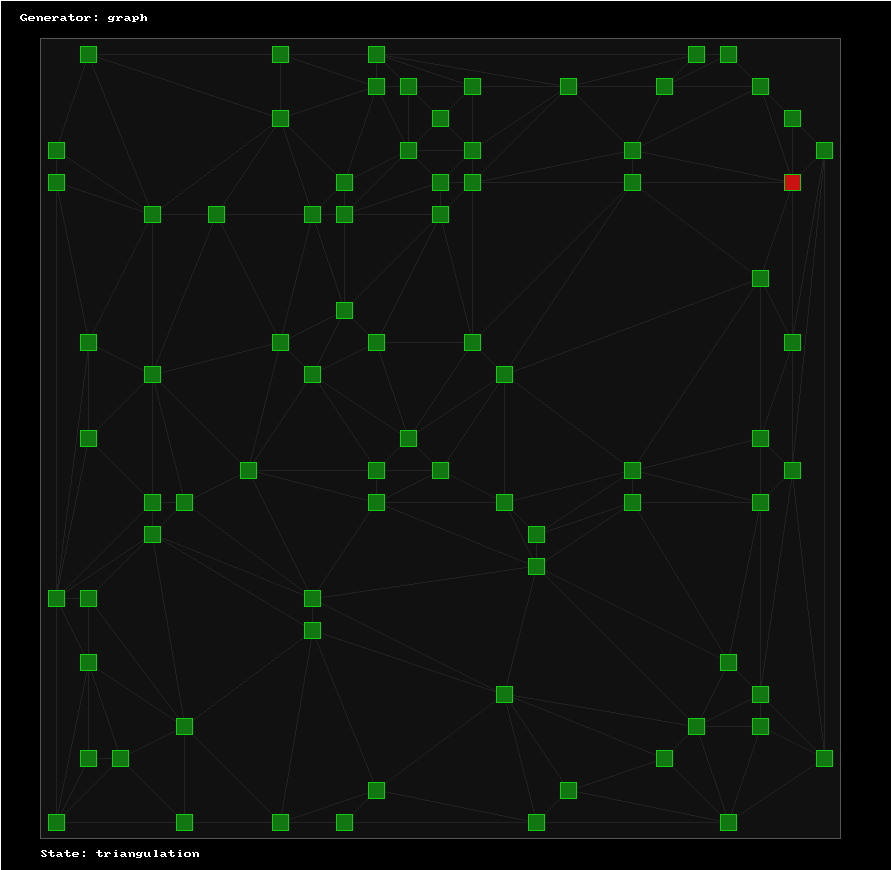

Then, extract a random spanning tree. The red node represents the root of the tree.

Then, compute the number of grandchildren for each node.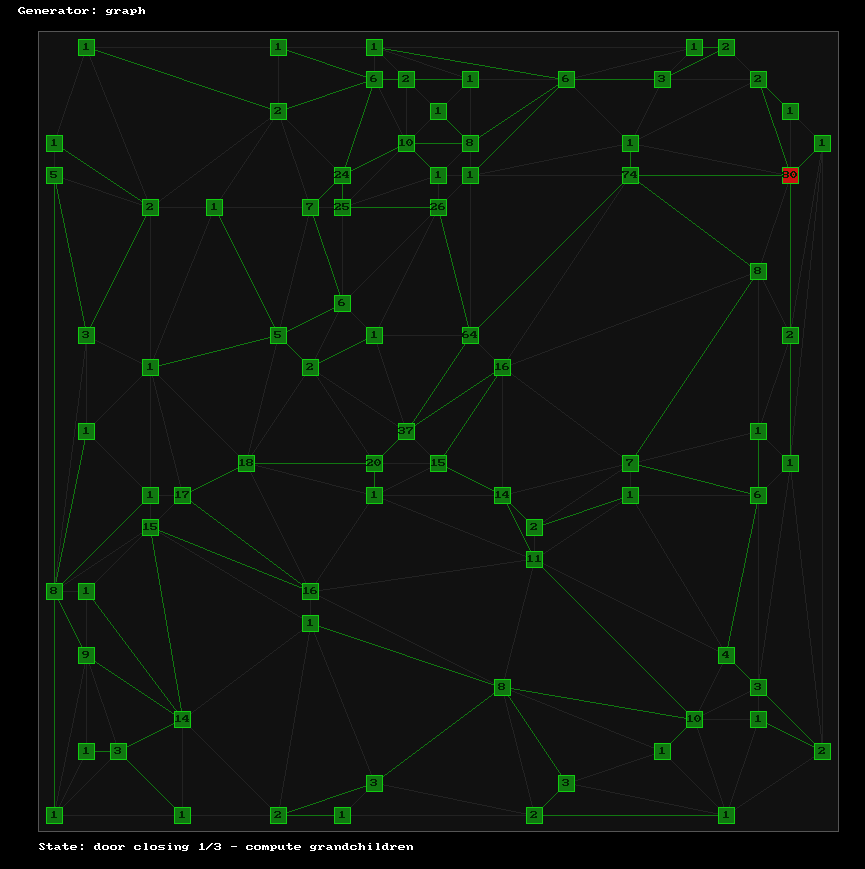

Find a node having a number of grandchildren nearly equal to 1/4 of the node count. This is the red-circled one, having exactly 20 children.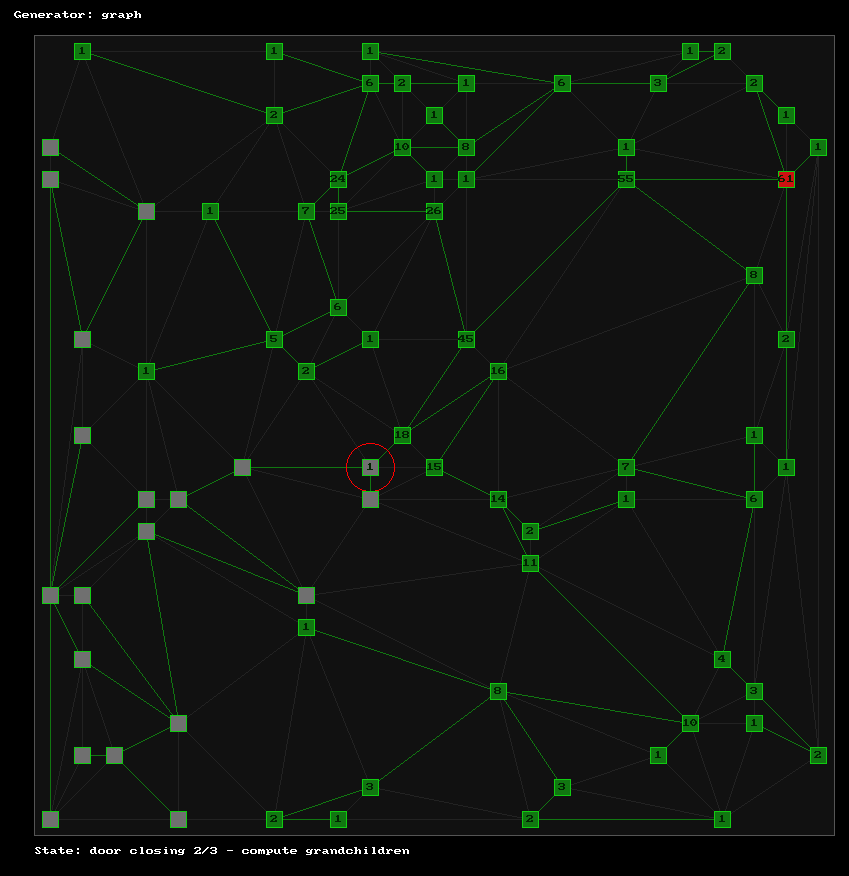

Next, repeat the operation.

Repeat a third - and last - time. The maze is now divided into nearly equally-sized areas.

In the beginning, my state-machine implementation looked like this:

class MazeGenerator
{
public:
  this()
  {
    m_state = STATE_INIT;
  }

  void oneStep()
  {
    switch(m_state)
    {
      case STATE_INIT:
        createPlanarGraph();
        m_state = STATE_PLANARGRAPH;
        break;
      case STATE_PLANARGRAPH:
        createSpanningTree();
        m_state = STATE_SPANNINGTREE;
        break;
      case STATE_SPANNINGTREE:
        createDoors();
        m_state = STATE_DONE;
        break;
    }
  }
private:
  STATE m_state;

  void createPlanarGraph();
  void computeSpanningTree();
  void createDoors();
}

However, I got the feeling something was wrong. Especially when I started to want to visualize how each individual door was chosen. Using an enum/switch introduces great friction when trying to add new steps to the generation algorithm. Dividing a step into two substeps is painfull, having variable number of steps is inconvenient. It seemed like a good opportunity to play with fibers. Here’s how it goes:

class MazeGenerator
{
public:
  this()
  {
    m_fiber = new Fiber(&generate);
  }

  void oneStep()
  {
    m_fiber.call();
  }
private:
  void generate()
  {
    createPlanarGraph();
    Fiber.yield();
    createSpanningTree();
    Fiber.yield();
    createDoors();
  }

  void createPlanarGraph();
  void computeSpanningTree();
  void createDoors();
}

A lot simpler, isn’t it?

The whole maze generator sandbox project is available on Launchpad: link

The source file corresponding to the very technique described in this article is here.

The Complexity Elephant

Topics

Software Development

Collision detection

Procedural content generation

Software Security

Meta

1. Generating mazes part 1 : using fibers to prototype the graph generation

2. Comments