The Complexity Elephant

Thoughts about software engineering, and game development.

Topics

1. Smooth collisions part 1 : disk versus segment

TL,DR: The full code is at https://github.com/Ace17/collide2d/tree/disk_vs_segment and is 80 line long. There’s also an interactive standalone SDL demo to play with.

Graceful collision response in a game can be tricky to implement. Even when all your objects are AABBs (axis aligned bounding boxes), problems arise as soon as you try to react to collisions in a non-trivial way.

If your game is a side-scrolling platformer, like Super Mario Bros, you might want your main character to smoothly walk on adjacent blocks.

If your game is a top-down RPG, like The Legend of Zelda, you might want your main character to smoothly slide along walls. You might also want it not to get stuck on salient corners.

Today, we implement collision detection and response for a disk of fixed radius, moving inside a set of solid segments, as shown below.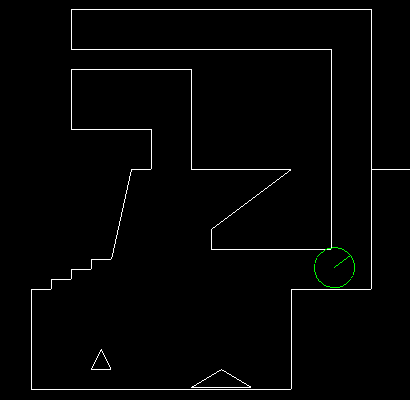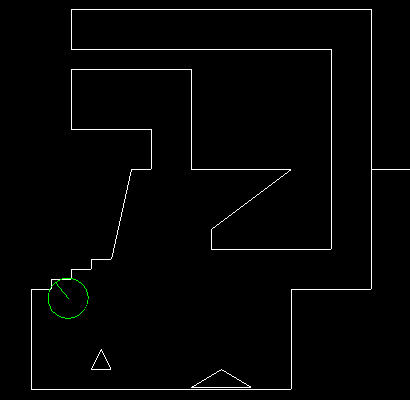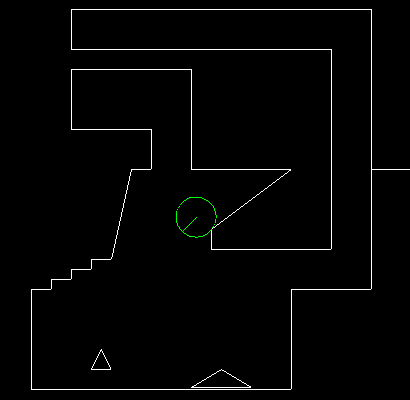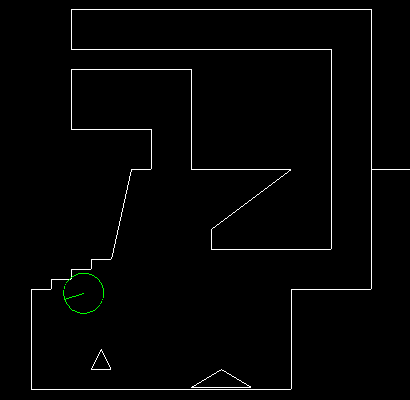

After cloning the repository, you can run ./run.sh to launch the demo. The keyboard mappings are:

up/down : move forward/backward
left/right : rotate
space : switch shape
origin : disable collisions (as long as the key is pressed)
esc : quit

This requires very little math knowledge (only basic vector algebra is required), and it’s rewarding and fun!

2. Collision response

We start with collision response. We’re not making a fully fledge physics engine here, so it will only push the disk enough to resolve the collision. We won’t deal with velocity, or anything related to time.

The function slideMove is the entry point to our "physics" code. It calls the collision detection code, collideWithSegments, and provides basic collision response.

It takes as input a starting position pos, and a "wanted" move vector delta.

It also takes the list of segments we want to test collisions against.

When it returns, pos is updated with the new non-colliding position.

void slideMove(Vec2& pos, Vec2 delta, span<Segment> segments)
{
  // move to new position ...
  pos += delta;

  // ... then fix it, if needed
  for(int i = 0; i < 5; ++i)
  {
    auto const collision = collideWithSegments(pos, segments);

    if(collision.depth == 0)
      break; // all collisions are resolved

    // fixup position: push the disk out of the segment
    pos += collision.N * collision.depth;
  }
}

The idea is dead simple: we force the new position, and patch it, until it’s not colliding anymore. Or until we reach the arbitrary limit on iteration count. We’re using discrete collision detection, so simultaneous collisions are probable. We might need a couple of iterations to handle them.

Please note that we might miss collisions if objects are moving too fast. I won’t go into this problem here, which is out of our scope today.

Note that there’s nothing in this function that actually depends on segments. This code just passes them through, and is actually agnostic to what they’re made of. Also, nothing depends on the fact that we’re dealing with a disk.

Now, we need a routine to actually detect - and measure - collisions.

3. Collision detection

3.1. Disk/segment collision

The following code computes one collision between a disk and a segment. The disk has a radius of RAY.

We first compute the segment’s closest point to the disk center. delta represents the vector going from the closest point to the disk center. If the length of delta is more than RAY, the disk is too far: we exit with no collision.

Otherwise, we return the following collision:

the collision depth is the disk radius, minus the length of delta.
the collision normal is the normalization of delta.

Collision collideDiskWithSegment(Vec2 diskCenter, Segment seg)
{
  auto const delta = diskCenter - closestPointOnSegment(diskCenter, seg);

  if(delta * delta > RAY * RAY)
    return Collision {};

  auto const dist = magnitude(delta);
  auto const N = delta * (1.0 / dist);
  return Collision { RAY - dist, N };
}

Please note we’re never using the segment’s normal. This is what allows a smooth collision response (i.e sliding) when the disk touches the extremity of a segment.

Please also note that, by comparing the squared distance, we avoid the costly call to magnitude (think: sqrt) in most cases here.

3.2. Nearest point on a segment

So we’re left with one last problem to solve: getting the point from a given segment [a;b] that’s closest to a given point P.

Let L be the infinite axis going through a and b, oriented from a to b. Let I be the orthogonal projection of P on L. Let tangent be the vector going from a to b.

If the scalar product (P - a) * tangent is negative, this means that I doesn’t lie on [a;b], it’s "before" a. In this case, the nearest point to P is a.
If the scalar product (P - b) * tangent is positive, this means that I doesn’t lie on [a;b], it’s "after" b. In this case, the nearest point to P is b.
Otherwise I lies on [a;b]: compute it, and return it.

(Note that we avoid the costly call to normalize in most cases here).

// returns the point from the segment 'seg' which is the closest to 'P'
Vec2 closestPointOnSegment(Vec2 P, Segment seg)
{
  auto const tangent = seg.b - seg.a;

  if((P - seg.a) * tangent <= 0)
    return seg.a; // 'P' is before 'a' on the line (ab)

  if((P - seg.b) * tangent >= 0)
    return seg.b; // 'P' is after 'b' on the line (ab)

  auto const T = normalize(tangent);
  auto const relativePos = P - seg.a;
  return seg.a + T * (T * relativePos);
}

4. Dealing with simultaneous collisions

There’s still on thing we need to deal with. What if the disk intersects two segments at the same time? Do we simply return the first one we find?

Actually, doing this doesn’t work here. If you do this, your disk is going to get stuck on extra vertices.

Let’s consider the following situation: the floor is perfectly flat and horizontal, but composed of two segments A and B.

Now suppose the disk goes from the non-colliding previous C position to the colliding C position.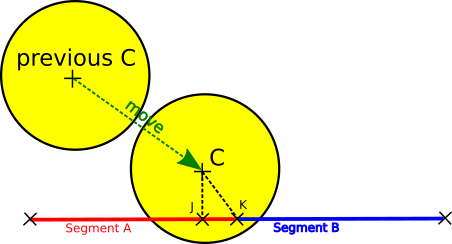

Now we’re colliding with both A and B. The problem is, we don’t get the same collision normal, depending on whether we choose to collide with A or B. Let J and K be the closests points to C, on segments A and B.

If we decide to collide with A, then we compute a collision normal as the normalization of the JC vector. This vector is perfectly vertical, which leads to a perfectly vertical upward repulsion. This is what we want.

If we decide to collide with B, then we compute a collision normal as the normalization of the KC vector. This vector is mostly vertical, but also has a slight horizontal component to the left. If the disk is sliding along the ground, from left to right, slowly enough, this horizontal component could compensate the horizontal move. In practice, the disk would get stuck when reaching K.

To avoid this, we always start by resolving the collision with the deepest penetration:

Collision collideWithSegments(Vec2 pos, span<Segment> segments)
{
  Collision deepest;

  for(auto seg : segments)
  {
    auto const collision = collideDiskWithSegment(pos, seg);

    if(collision.depth > deepest.depth)
      deepest = collision;
  }

  return deepest;
}

If you want to see for yourself why this selection is needed, simply neutralize the above condition, in order to always reassign deepest, and then launch the demo program. Now try to slowly slide upwards along the rightmost vertical wall. If you slide slowly enough, you will get stuck halfway.

At this point, I must confess, I’m not sure this is the correct way of doing things. It might be possible to create a situation where taking the shallowest penetration would be the right answer. However, I wasn’t able to find one, and this strategy seems to work in practice.

5. Putting it all together

The full source code is in the github repository, in the "disk_vs_segment" branch:

https://github.com/Ace17/collide2d/blob/disk_vs_segment/collision.cpp

This code is simple and robust ; unlike continuous collision detection, it deals gracefully with invalid initial configurations, and will resolve smoothly any already-penetrating state.

Even cooler: it also gracefully handles moving segments, or a dynamically disk radius (provided they don’t change too fast).

At this point, you should be able to write the physics for a 2D polygon-based top-down shooter, like Doom!

In the next post, I’ll explain how to extend this collision code to handle axis-aligned bounding boxes.

Stay tuned!

The Complexity Elephant

Topics

Software Development

Collision detection

Procedural content generation

Software Security

Meta